
Team Name: TAPLAS
Is O'Caml still the programming tool of choice for discriminating hackers?
Members: Yutaka Oiwa, Akihito Nagata, Tatsurou Sekiguchi, Masashi Seiki
Program Name: T2003-GA (written in Objective Caml)
We loose the game... Our results were far from the winner's result. This year I have encouraged our junior students, to whom I teach Objective Caml language in the programming education course, to join the contest and they formed the team, but they have gave up to implement an automatic solution. However, very unfortunately, their "fully manual" result is far better than we can achieve! They had written an "undo-able" interactive racing program and playing the racing game all over the days and nights...
We dare to keep that our program is fully-automatic, i.e. the program does not need any course-specific data except for course map itself. However, we could not even catch up with their car, and the 72-hour Grandprix is chequer-flagged. I was a bit wondering that the phrase "Hand optimizing is the program tool of choice for discriminating hackers" comes true or not. So hearing at the Uppsala that the automatic program written in C++ wins the contest is something bitter-sweet for me (Yutaka).
Any way, this is our entry for the 2003 ICFP Programming Contest. I hope that we can do much better in 2004...
As Eijiro Sumii is moved to the University of Pennsylvania from April 2003, we invited a new member Akihito Nagata, a master student in our research group. In the final day, another master student Masashi Seiki had joined and helped our work.
The goal of this year's ICFP Programming Contest is simple: to control a racing car in a given circuits and reach the goals. The complete task description is published in the Programming Contest Homepage.
The source code is under preparation for publication...
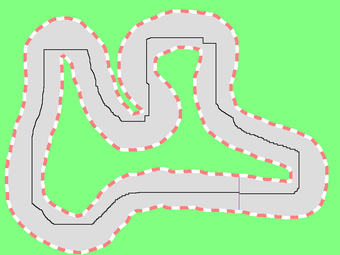
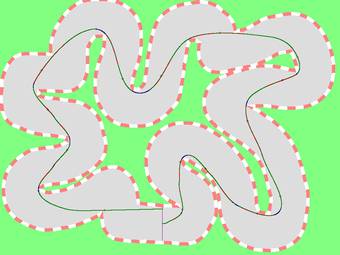
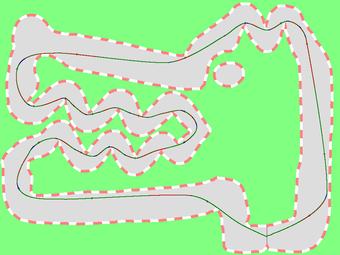
The following pictures are the traces of our solutions.
1: 10841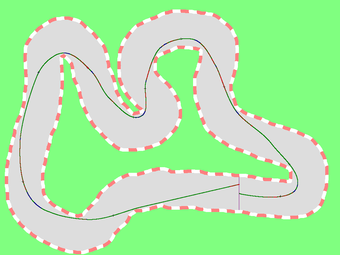

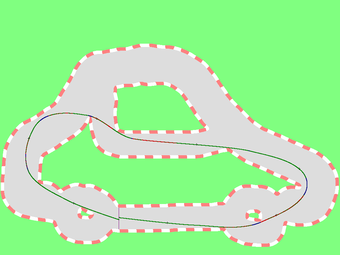
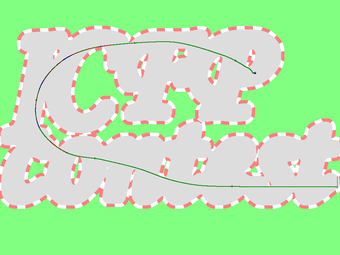
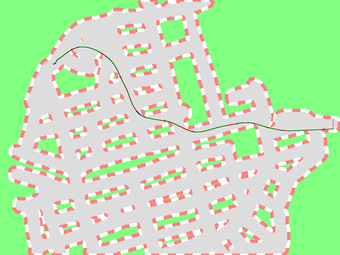
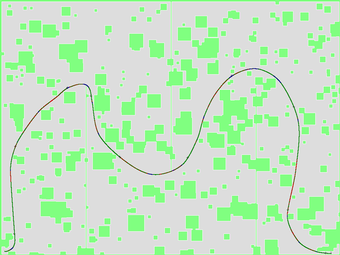

Roughly speaking, our program is constructed by three different components: one for finding possible path, one for tracing the given path without hitting walls, and one for optimizing the path. We describe the strategies in each part of program in order.
At first the program makes a rough plan. The path-finding routine firstly searches the whole racing field to find a possibly-fast route. We have reused the implementation of the Dijkstra algorithm from the the previous year's program. This year, the cost estimation is based on the radius of the open space around each point: passing narrow pathways, or running near the wall have big cost penalties at this stage.
| Figure 1. the paths found by Dijkstra algorithm |
|---|


|
The path found by the Dijkstra method have only diagonal moves, which is far from the optimal running course. We postprocess the resulting path, by removing as many as points as possible from the path iteratively and connect gaps by spline curves. The processed path is now made of smoothly-connected spline curve segments. Finally we divide each spline segments to a list of shorter segments (approx. 1 ~ 2 pixels in length).
| Figure 2. the paths fitted by Spline curves |
|---|
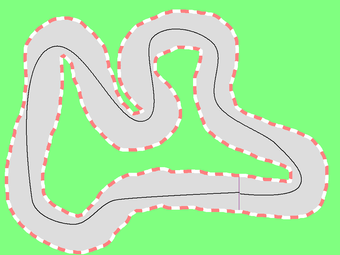

|
Nextly, we convert the path to a list of car-controlling commands. There are many things we must consider.
The first problem is "turning on a curve": the over-speeding in a curve
make car going outside and crashing. Our solution is to calculate a
possible max speed for each path segments based on the curvature of it.
Presuming that the car keeps constant speed v and keeps steering to right,
the car goes on a circle of radius
The next problem is "braking": As cars can't stop immediately, we must precaution about any steep curves which are beyond our path. Before actually running the car on the course, our program scans the course in the reversed direction and searches for the speed-limiting curves. For each segments, the scanning process compares the possible maximum speed of the current segments to that of the next segment. If the speed for the current segment is slower than the next's one, that is OK. However, if the speed for the current segment is faster than the next segment's speed, the speed limit for the current segment is reduced based on the next segment's speed.
Given the length of a segment, the terminal speed, and whether we use disc brakes or not (only use wind dragging), the possible entrance speed of the segment can be calculated by solving integral equations. We solve the integral equations using numerical method. The tactical problem here is whether to use brake or not, as the rule forbids to use steering and braking simultaneously. Our solution is:
After the decellation is estimated, the speed limit for the current segment is reduced to the sum of the speed on next segment and the possible decellation in the current segment.
| Figure 3. the speed limits on route |
|---|
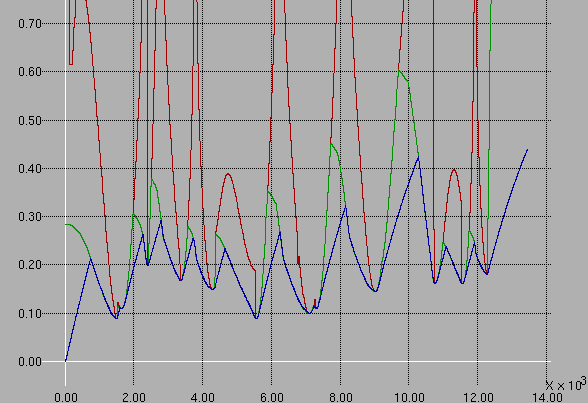 |
| X axis is the total length from the start of the route. The red line: the speed limit estimated from curvatures. The green line: the speed limit considering braking distances. The blue line: the actual car speed. |
A small noticible point: We must use fixed-point arithmetic specified in the rule when calculating a dragging force. The dragging forces calculated during simulation is noticiblly smaller than mathematically-correct values because of rounding errors.
After determining the possible speeds and the method for decellation, We run the simulated car on the circuits.
The steering direction is basically determined on the estimated gap from the desired route after 10 turns passed from the current tick. However, as the response of steering of the car is very bad, it is very easy to make too many steering and snakes the way. Therefore, if the direction of the velocity of the car is too much different from the direction of the route to be corrected before crossing over the desired route, a correction is given to restore the velocity direction.
The acceleration is controlled by comparing current speed with the possible maximal speed which is already estimated in the previous "braking" section. If the braking analysis suggests use of the brake, we use brake only when the derivation of the current position from the desired route is less than one pixel. This makes hybrid use of brake and steering while running on curves.
Now we have one solution to the task. The final task is to optimize the route to achieve better result. We uses genetic programming method to solve this problem. The genes encoding is the list of the coordination of the control points of a spline, and the value of the genes are the ticks needed to run the car on routes specified by genes.
The method of mutation is somewhat specific to the contest task. By this encoding of the genes, mutating the position of a control point may not be sufficient to make better route: when the route in curve or the straight line are too loose or too tight, moving moving two control points before and after the concerned section in the parallel direction is very useful. Therefore, our mutation process randomly chooses either one control point or two (or sometimes three) successive control points from the gene, and moves those points by the same random vector.
Our research group has insensitively parallel computers like Sun UltraEnterprise 4500 (14 UltraSparc-2 CPUs) and IBM NetFinity 7100 (4 Pentium-3 CPUs). We have parallel run 10 programs in parallel (one for each course) overnights to get optimized result, although the program itself does not use more than 1 CPU.
| Figure 5. the paths before and after optimization |
|---|
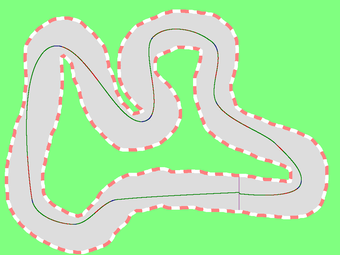

|
This year, we have used CVS to share the source. Yutaka implemented routines for course parsing, first path finding, curve tracing, and mutation of the gene in the genetic algorithm. Akihito implemented routines for spline generation and reduction, global optimization using genetic algorithm, and a visualization program which is useful for debugging and tuning the parameters. Tatsurou have tried to implement a drastic method for route optimization: insensitive search for all possible movements with edge reaping. However, that routine is not used to make the final submission because of intensive CPU usage and time limitation. Masashi have caught into team at the timing of final 12 hours, and helped us the final optimization and other works.
We have used given ten circuits and mathematically-generated circular route to verifies and repeatedly optimize the algorithms. However, the resulting program does not need any additional information about the course: one program solves the problem on all ten circuits and hopefully on any other courses.
Almost obvious: T stands for TAPLAS (name of the team and the domain-name of our research group), 2003 stands for year 2003, GA stands for genetic algorithm.